Voici un petit utilitaire pour tracer les courbes mais pas uniquement : Grapher. Certains connaissaient CurvusPro de chez Arizona-Software qui propose toujours une version, dorénavant gratuite pour classic. Mon but est de montrer deux, trois astuces d'utilisation de ce fabuleux programme.
Le choix du document :
On va pour notre premier essai créer une courbe plane dans un repère standard.
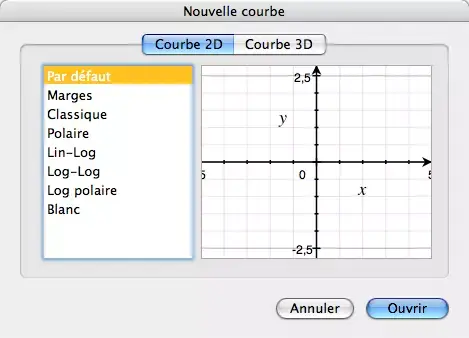
D'autres choix sont disponibles, du papier semi-logarithmique :
au papier pour les courbes polaires :
Le choix du repère peut-être modifié ultérieurement. La seule chose à bien choisir est la dimension du domaine de travail 2D ou 3D...
Un petit outil bien pratique : Égaliser les axes permet comme son nom l'indique d'uniformiser le repère, ce qui est indispensable si l'on veut respecter les angles ou faire qu'un cercle resemble à un cercle. Comme le montre les deux exemples ci-dessous :
Différents types de courbe et syntaxe :
• Le plus simple y=sinx trace la représentation graphique de la fonction sinus. Vous remarquerez que même sans parenthèses ni espace, le programme met le x en italique et que le nom de la fonction en roman. La mesure d'angle par défaut est le radian mais on peut en changer dans les préférences. Dans le menu Préférences / Onglet "Avancé" : ce trouve le petit menu ci-dessous :
Si l'on clique près de la courbe, les coordonnées du point le plus proche s'affichent.
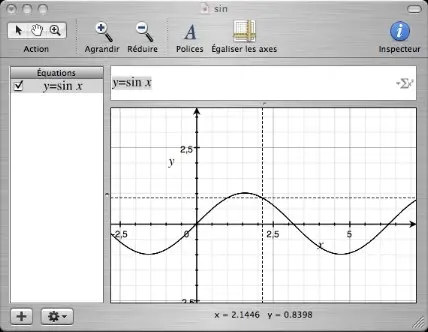
L'inspecteur permet de changer l'apparence de la courbe (couleurs, épaisseur du trait, ...)
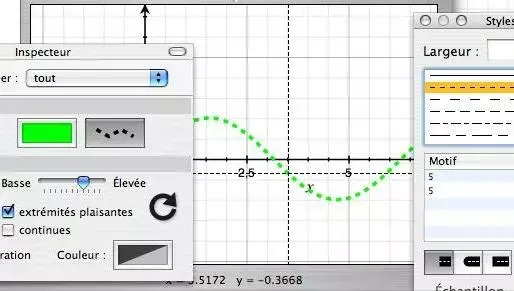
Pour une analyse un peu plus poussée, dans le menu Équation se trouve un article intitulé Évaluation. On a alors la valeur mais aussi l'interprétation graphique de la fonction (le point), de la dérivée (la droite tangente) et de la dérivée seconde (la courbure).
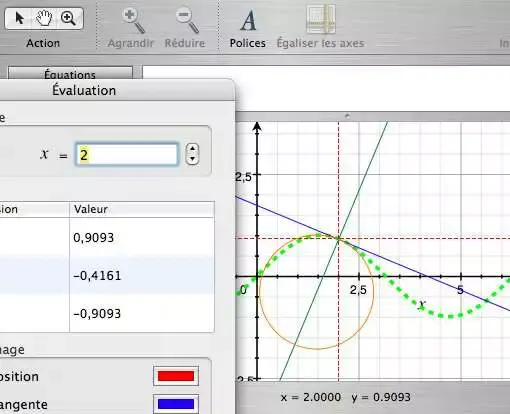
On a aussi un article Intégration, où l'on peut soit entrer des valeurs, soit cliquer directement sur la courbe le domaine. (Un menu permet d'entrer les bornes -infini +infini)
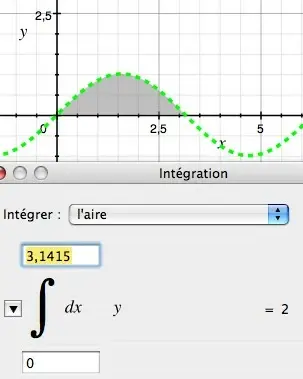
• Autre formulation r=3theta. Dès qu'on a fini de taper les lettres de theta, on se retrouve avec une jolie lettre grecque. Cette formulation permet de tracer une courbe en équation polaire.
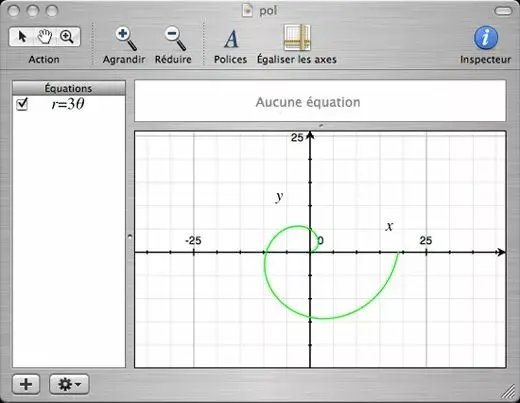
Le seul reproche est que le domaine des angles est défini dans les préférences. De plus dans les exemples, dans les modèles proposés ainsi que dans les préférences, ils utilisent la lettre phi alors que c'est la lettre theta. Ainsi dans l'exemple ci-dessous la restriction à un domaine d'amplitude 2pi montre la limite :
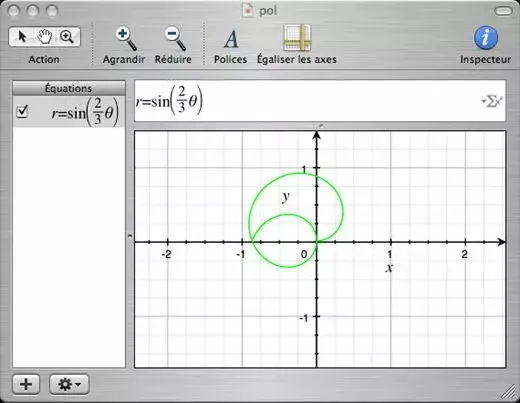
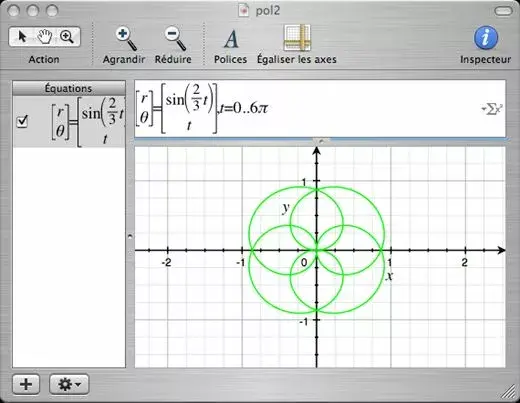
• Pour palier à ce problème on peut passer par les courbes paramètriques dont la syntaxe est [x y] ou [r theta] = ... selon que l'on choisisse les coordonnées cartésiennes ou polaires. Le domaine du paramètre t est indiqué après la formule avec une virgule, et deux points entre les bornes.
• En dehors des courbes, Grapher permet de donner et de définir des constantes, des ensembles de valeurs et même des fonctions. Ces définitions sont caractérisées par un petit rond vert .
Voici un petit exemple :
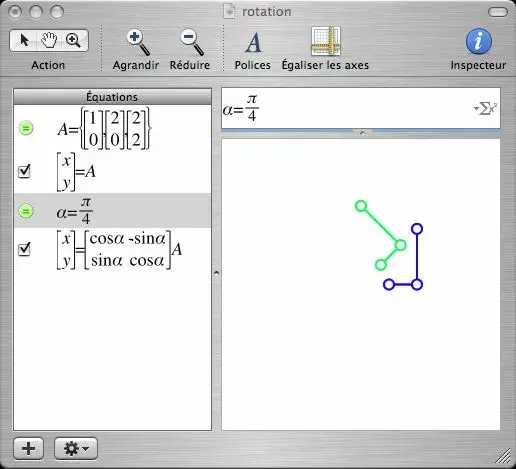
Ligne à ligne :
- A={[1 0],[2 0],[2 2]} - defini un ensemble de trois points. - [x y]=A - trace les points de l'ensemble A. - alpha=pi/4 - défini un angle alpha (étonnant non !) - [x y]=[.....]A - trace les points après avoir appliqué un calcul matriciel (ici matrice de la rotation d'angle alpha)
(Si l'image paraît déformée, il faut cliquer sur "Égaliser les axes")
Remarque : Si l'on renomme le paramètre alpha en t, le nom change aussi dans la matrice !
Le gros avantage des paramètres, comme ici, est quel'on peut créer une animation. Soit par le menu Animation de paramètre ou Création animation.... Dans notre exemple, il faut mettre une valeur numérique genre alpha=3,1415 plutôt que pi, pour que ce choix puisse s'activer.
Un exemple un peu plus poussé :
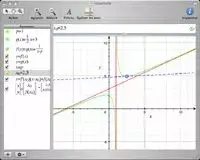
Dans cet exemple, on a séparé la définition des fonctions et le tracé de ces dernières ce qui facilite les modifications ultérieures. Pour mettre un nombre en indice comme x0, il faut utiliser le _ (le souligné), c'est comme sous TeX. On remarque aussi que pour tracer la tangente à la courbe en x0, il "suffit" de mettre y=f'(x0)(x-x0)+f(x0), c'est à dire que Grapher calcule lui-même la dérivé.
En espérant que tout ceci sera utile à certains... Le programme est très pratique et j'espère qu'Apple continuera à l'améliorer, il y a encore trop de bugs, comme par exemple la taille du document qui n'est pas sauvegardé. On crée un document de 10 cm sur 10 cm, on place un d à côté d'une droite (logique) et quand on re-ouvre le document, la taille est de modifiée et le d n'est plus à sa place... Ils ont piqué ça aux Suisses, ce n'est pas pour en arrêter le développement !
